极限的定义

极限描述了函数在特定点附近的行为，而不一定是点本身

极限的存在性

当且仅当单侧极限$\lim\limits_{x \to 2^-}$f(x)与$\lim\limits_{x \to 2^+}f(x)$存在且相等时
双侧极限$\lim\limits_{x \to 2}$f(x)存在

极限的计算

对于任何常数k，（例如）$\lim\limits_{x \to c}=k(3.1)$

此时，其极限为c
常数的极限是其本身

定理3.1

假设$\lim\limits_{x \to c}f(x)$和$\lim\limits_{x \to c}g(x)$均存在，且c为任意常数
则以下皆成立

$\displaystyle\lim\limits_{x \to a}[c * f(x)]=c * \lim\limits_{x \to a}f(x)$
$\displaystyle\lim\limits_{x \to a}[f(x)±g(x)]=[\lim\limits_{x \to a}f(x)]±[\lim\limits_{x \to a}g(x)]$
$\displaystyle\lim\limits_{x \to a}[f(x) * g(x)]=[\lim\limits_{x \to a}f(x)][\lim\limits_{x \to a}g(x)]$
$\displaystyle\lim\limits_{x \to a}\frac{f{x}}{g{x}}=\frac{\lim\limits_{x \to a}f(x)}{\lim\limits_{x \to a}g(x)}\quad (\lim\limits_{x \to a}g(x)≠0)$

定义3.2

如果p(x)和q(x)是多项式，则$\lim\limits_{x \to c}p(x)=p(c)$
且$\displaystyle\lim\limits_{x \to c}\frac{p(x)}{q(x)}=\frac{p(c)}{q(c)}$，当$q(c)≠0$时

定义3.3

假设$\lim\limits_{x \to a}f(x)=L$且n为任意正整数，则

$\displaystyle\lim\limits_{x \to a}^n\sqrt{f(x)} = ^n\sqrt{\lim\limits_{x \to a}f(x)}=^n\sqrt L$

其中，n∈任意正整数，且L>0

定义3.4

对于任意实数A，我们有

$\lim\limits_{x \to a}sinx=sina$
$\lim\limits_{x \to a}cosx=cosa$
$\lim\limits_{x \to a}cosx=e^a$
$\lim\limits_{x \to a}lnx=lna\quad(a>0)$
$\lim\limits_{x \to a}sin^-1x=sin^-1a\quad (-1<a<1)$
$\lim\limits_{x \to a}cos^-1x=cos^-1a\quad (-1<a<1)$
$\lim\limits_{x \to a}tan^1x=tan^-1a\quad (- ∞<a<∞)$
如果p是多项式且$\lim\limits_{x \to p(a)}f(x)=L$,则$\lim\limits_{x \to a}f(p(x))=L$

夹逼定理

定义3.5

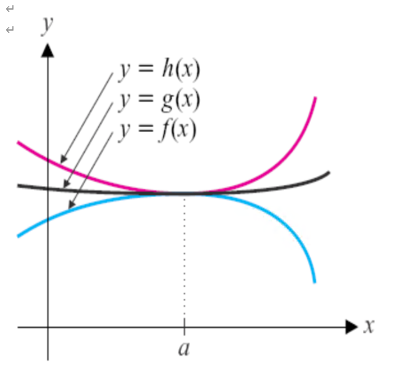
人话：
这个定理用于求一个函数的极限
当这个函数被两个具有同极限的函数夹在中间时
$f(x)≤g(x)≤h(x)$
当x趋近某个值时，f(x)与h(x)极限相等，那么g(x)的极限也是这个值

定义：
假设有$f(x)≤g(x)≤h(x)$
如果在某个区间 $(c, d)$ 内，除了点 (c) 以外的所有 (x)，满足
$\lim\limits_{{x \to c}} f(x) = \lim\limits_{{x \to c}} h(x) = L$
对于某个数 (L)，并且 $[ g(x) \leq f(x) \leq h(x) ]$ 在该区间内的所有 (x)，除了点 (c) 以外，那么 $[ \lim\limits_{{x \to c}} g(x) = L ]$

函数的连续性

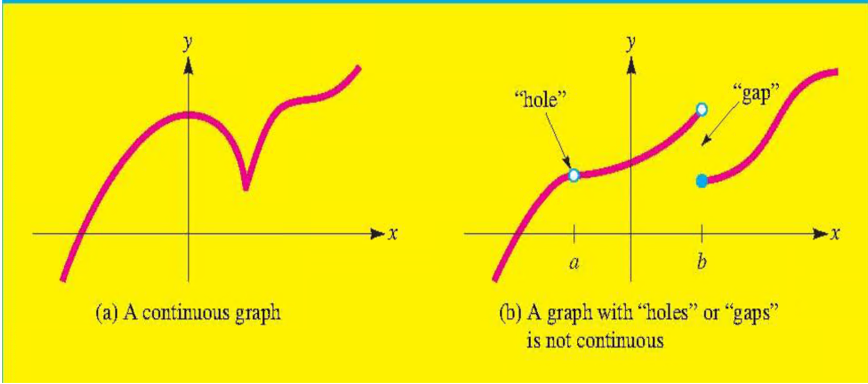
连续函数是指“一笔画完的函数”（笔不离开纸）
a. 一个连续的函数
b. 一个具有洞和断点的函数不连续

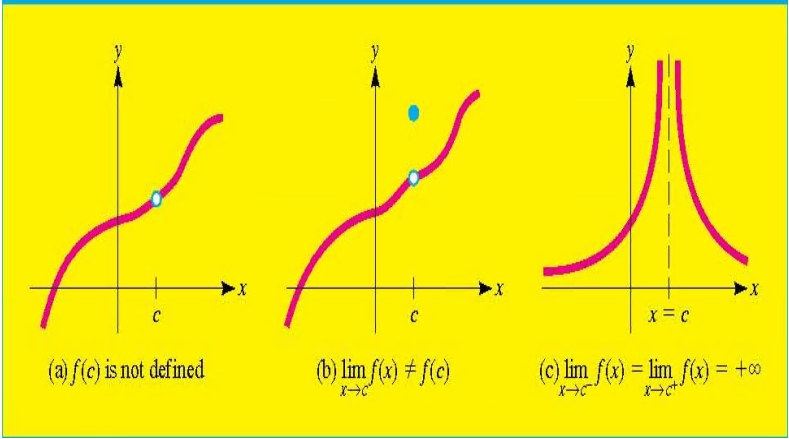
在x=c处，函数有一个“洞”(hole)
a. 在这个点的位置，函数没有被定义
b. 点并不在函数线上，所以极限的数值那个位置与原函数不相等
c. 在极限的位置，函数趋于正无穷

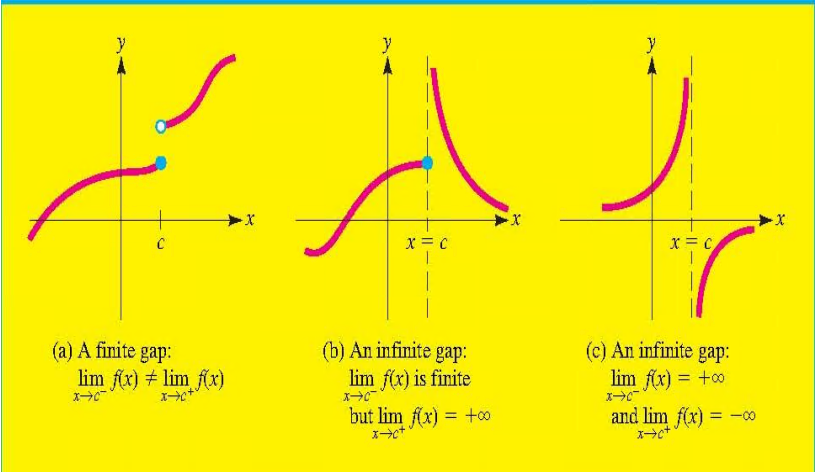
在x=c处，函数有一个断点(gap)
a. 一个有限的间隙
b. $\lim\limits_{x \to c^-}f(x)$趋于正无穷
而另一端的极限则具有实数解
c.$\lim\limits_{x \to c^-}f(x)$趋于正无穷
另一端则趋于负无穷

定义4.1

若函数$f$在$c$处是连续的，则必须满足以下三个条件

$f(c)$被定义
$\lim\limits_{x \to c}f(x)$极限存在
$\lim\limits_{x \to c}f(x)$=$f(c)$

如果$f(x)在c处不连续，则称其在那里具有不连续性$
当可以通过定义该点的函数来消除不连续性，我们称该不连续性是可消除的
(discontinuity removeable)
并非所有不连续性都可以被消除

连续性多项式和有理函数

如果$p(x)和q(x)是多项式，那么

$\lim\limits_{x \to c}p(x)=p(c)$
$\displaystyle\lim\limits_{x \to c}\frac{p(x)}{q(x)}=\frac{p(c)}{q(c)}\quad if q(c)≠0$

多项式或有理函数在任何地方定义都是连续的

定理4.1

所有多项式都是处处连续的。
$sinx$、$cosx$、$tan^-1x$和$ex$都是处处连续的
当n是偶数时，$^n\sqrt x$在所有x都是连续（x≥0）
当n为奇数时，$^n\sqrt x$在所有x上连续
函数$ln x$在x>0时连续，tanx和secx在$-\frac{\pi}{2}<x<\frac{\pi}{2}$时连续

定理4.2

如果函数f和g在a点连续，则下列结论成立：

f ± g在a点连续
f * g在a点连续
如果$g(a)≠0$,则$f * g$在a点连续

定理4.3

假设$\lim\limits_{x\to a}g(x)=L$，且函数f在L处连续，则

$\lim\limits_{x \to a}=f(\lim\limits_{x \to g}g(x))=f(L)$

推论4.1

假设函数f在z处连续，且函数g在f(z)处连续，那么复合函数$f \circ g$在z处连续

复合函数

$f \circ g$是一个复合函数，具体来说，是先应用后部的函数$g$，然后再把前部的函数$f$应用到$g$的结果上，具体来说，如果$h(x)=f(g(x))$，那么$h$==$f \circ g$

区间的连续性

如果f(x)在该区间的任何一点x=c上都是连续的，那么f(x)在开区间a<x<b上也是连续的
如果f在开区间a<x<b上是连续的，那么f在闭区间a≤x≤b上也是连续的,且
$\lim\limits_{x \to a^+}=f(a)\quad \lim\limits_{x \to b^-}f(x)=f(b)$
如果$f$在$(-∞，∞)$上是连续的，称之为$f$始终连续

中间值性质

定理4.4

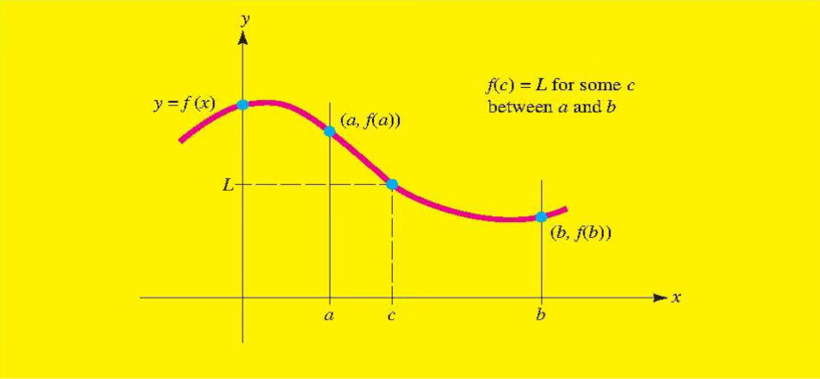
假设f(x)在a≤x≤b的区间上是连续的，1是f(a)和f(b)之间的一个数，则a和b之间存在一个数c，使得f(c)=1

推论4.2

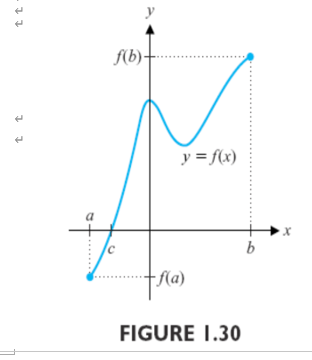
如果f在闭区间$[a,b]$上是连续的，且$f(a)$和$f(b)$有相反的符号（即$f(a)*f(b)＜0$）
则(a,b)中存在一个数c，f(c)=0

二分法

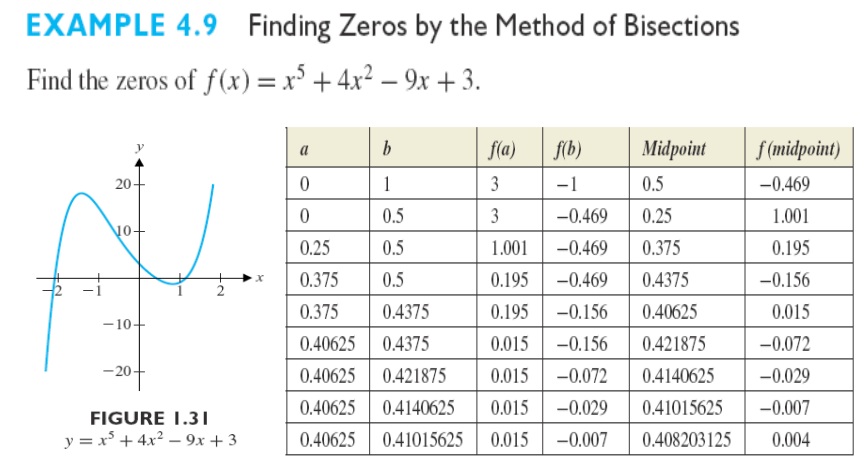
二分法可以帮助确定函数的零点

渐进线

当x趋于无穷大时，$\displaystyle\frac{1}{x}$趋向0

同样地，当e趋向无穷大时，$\displaystyle-\frac{1}{x}$趋向0

故认为$\displaystyle\lim\limits_{x \to 0^+}\frac{1}{x}$和$\lim\limits_{x \to 0^-}\frac{1}{x}$不存在

当极限不存在时，可以认为$\displaystyle\lim\limits_{x \to 0}(\frac{1}{x})$不存在

备注5.1

极限$\lim\limits_{x \to 0^+}(\frac{1}{x})$指的是当x从整数的一侧接近0时，函数$\frac{1}{x}$的值会变得越来越大
这个极限用∞表示，意思是当x接近0时，函数值趋向无穷大
尽管我们写成了$\displaystyle\lim\limits_{x \to 0^+}(\frac{1}{x})=∞$，但$∞$不是实数，不能说极限存在于实数范围内。
当我们说极限不存在时，指的是没有一个实际的实数L使得函数值趋近。
用$∞$只是表示函数值会无限增长

备注5.2

以下表达式 $\displaystyle\lim\limits_{x \to 0}\frac{1}{x^2}=∞$表达的是：

当x接近0时，$\displaystyle\frac{1}{x^2}$的值会变得无限大

相比之下，说$\displaystyle\lim\limits_{x \to 0}\frac{1}{x^2}$不存在只能表明极限不存在，而不能说明$\displaystyle\frac{1}{x*2}$随x接近0的变化趋势
前者不仅表明了极限不存在，还更明确地指出了函数值在x接近 0 时趋向于无穷。

垂直渐近线

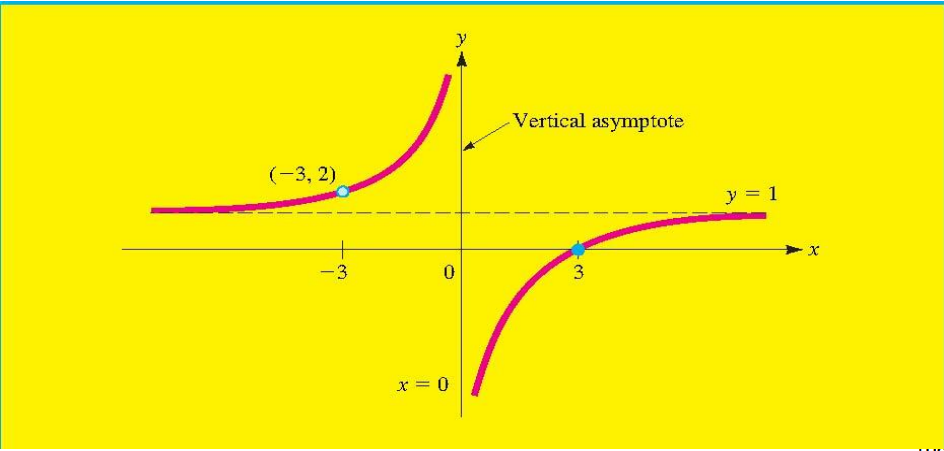
此图像描述了垂直渐近线的概念，特别是关于函数$f(x)$在$x=0$附近的行为
如果有一函数$f(x)=\displaystyle\frac{x^{2}-9}{x^{2}+3x}$

其中$p(x)=x^{2}-9$和

$q(x)=x^{2}+3x$

当x=0时，分母q(0)=0，但分子p(0)≠0

当x=0时，分母q(0)=0，但分子p(0)≠0
这意味着在x=0处，函数f(x)有一条垂直渐近线，直线x=0

垂直渐近线是一种在函数图形中，当 x 接近某个特定值 c 时，函数值会趋近于无穷大的直线。
更具体地，当 x=c 是函数 f(x)的垂直渐近线时，无论 x 从左还是从右接近 c
函数 f(x)的值都会变得无穷大或无穷小

无穷处极限

当函数f(x)的自变量x无限大时，如果f(x)接近一个固定的数值L，我们就说函数在x趋向于正无穷时的极限是L

表示为：$\displaystyle\lim\limits_{x \to ∞}f(x)=L$

同样地，如果当自变量x无限小时，函数f(x)接近一个固定数M，则称函数在x趋向于负无穷时的极限是M

表示为表示为：$\displaystyle\lim\limits_{x \to -∞}f(x) = M$

例子：考虑函数f(x)=1/x
在这个情况下： - 当 x 越来越大（即 x → +∞），那么 1/x 将会接近0。
因此 lim (当 x → +∞ ) 1/x = 0。
类似地，当 x 越来越小且为负值（即 x → -∞），那么 1/x 同样也会接近0。
因此 lim (当 x → -∞ ) 1/x = 0

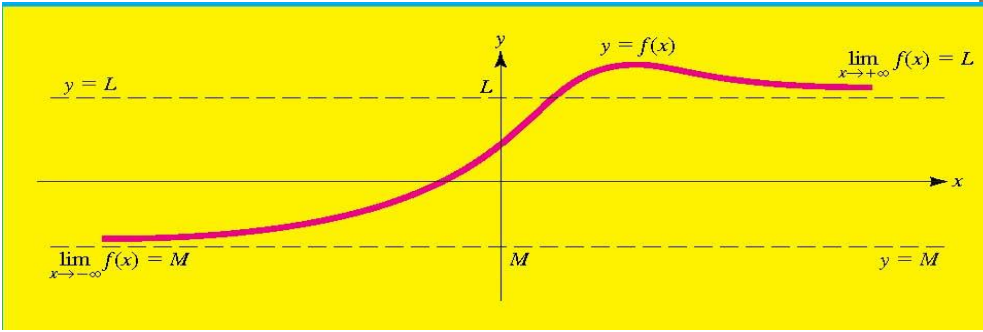
这张图片中展示的是关于水平渐近线（Horizontal Asymptotes）的定义。在数学上，如果一个函数f(x)当x趋向无穷大或负无穷大时，其极限值为常数b，则称直线y=b为该函数图像的水平渐近线。具体来说：

如果当x趋向正无穷大时，f(x)的极限是b，则y=b是右侧水平渐近线。
如果当x趋向负无穷大时，f(x)的极限也是b，则y=b同时也是左侧水平渐近线。

例如：对于函数 $\displaystyle f(x) = \frac{3}{x} + 4$ ，当x趋向正无穷或负无穷时，$\displaystyle \frac{3}{x}$趋于0

因此 $\displaystyle lim_{x\to\pm\infty} f(x) = 4$ ，所以 $y=4$ 就是这个函数图像的水平渐近线。

定理5.1

$\displaystyle\lim\limits_{x \to ±∞}\frac{1}{x^t}=0$

对于任何正有理数t，当x趋向于无穷大时，1除以x的t次方（即1/x^t）的极限是0。
也就是说，随着x值不断增加，分母会变得非常大，导致整个分数趋近于0。
对于当x趋向负无穷时的情况，则假设t=-p/q, 其中q为奇数。这里没有给出具体结论，但通常在处理极限问题时会根据函数特性来确定结果。

例子：如果我们取 t=2（也就是说我们考虑函数 f(x) = 1/x²），随着 x 的增加（例如 x=10,100,1000,...），f(x) 将会逐渐减小接近 0 （例如 f(10)=0.01, f(100)=0.0001, f(1000)=0.000001）。

定理5.2

对于任何正整数n和一个n次多项式函数p(x)，其形式为$p(x) = a_nx^n + a_{n-1}x^{n-1} + \dots + a_1x + a_0$，其中$a_n$是最高次项系数且不等于0。

该定理描述了当变量x趋向无穷大（即$x \rightarrow \infty )$时，多项式函数p(x)的极限行为。根据最高次项系数 (a_n) 的正负性有两种情况：

如果$a_n > 0$，那么当 $x \rightarrow ∞$, 多项式p(x)的极限值也会趋向无穷大。
如果$a_n < 0$，那么当 $x \rightarrow ∞$, 多项式p(x)的极限值会趋向负无穷。

例如：如果我们有一个三次多项式函数$p(x)=2x^3+3x2+x+5$，由于最高次项系数(也就是$a_3=2$)是正的，则根据此定理可知，随着x越来越大，这个三次多项式函数将会增长至正无穷大。

经验法则

求函数在无穷远处极限的法则——经验规则（Rule of Thumb）
计算方式如下

将函数$f(x)/g(x)$中的每一项都除以分母g(x)中出现的最高次幂。
利用代数性质计算极限$\lim\limits_{x \to +\infty}f(x)或\lim\limits_{x \to -\infty}f{x}$，通常是通过简化表达式来实现。

例如，如果有一个函数 $h(x)= (3x^3 + 7)/(2x^3 - x)$
我们要求当x趋于正无穷大时h(x)的极限。

按照经验规则，我们可以将分子和分母都除以$x^3$（因为它是分母中出现的最高次幂），得到
$(3 + 7/x^3)/(2 - 1/x^2)$。
随着x趋于无穷大，$7/x^3$ 和 $-1/x^2$ 这两项都将趋近于0，所以原始极限问题简化为$lim (x → ∞)(3/2)$，解为1.5

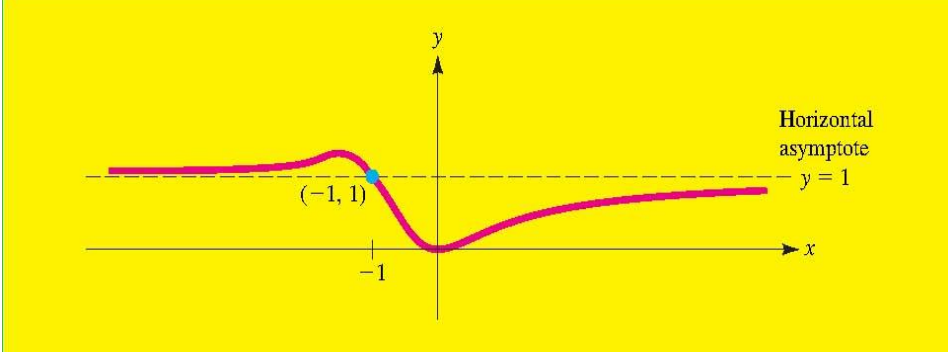
$f(x)$的图形以$y=l$为水平渐近线。

注：函数f(x)的图像永远不能越过垂直渐近线x=c，因为至少有一个单侧极限必须是无限的。
然而图像有可能越过它的水平渐近线。